Input-output and Output-output relations-based modal parameter estimator
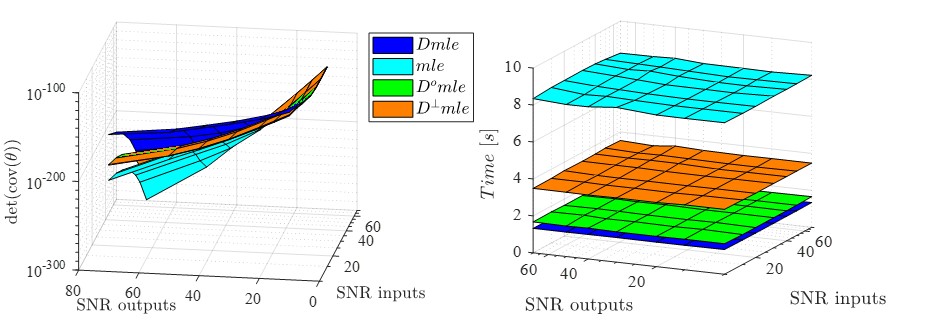
Recently the innovative identification group is developing new estimators strategies that allow exploiting all the data information that current methods (Experimental and Modal analysis –EMA and OMA) fail to do. More specifically OMA methods do not take into account input information while EMA methods considers disturbance inputs as noise. The new estimators are developed int the context of maximum likelihood Estimators (MLE) taking into account the possibility and its effects when the full noise information matrix is not available. The new estimators are assessed based on the covariance of the parameters, the convergence time and its efficiency.
Experimental Modal Analysis (EMA) identification methods and procedures are limited to forced excitation laboratory tests where the applied forces and system response can be measured. In many applications, however, the measurements have to be performed in “operational” conditions (Operational Modal Analysis – OMA) where the structure is excited by the natural (ambient) excitation sources. In such a case, the input forces are not taken into account and only output signals can be measured. The modal thus obtained will depend on the operational conditions.
Depending on the application is still possible to excite the system even when the excitation signal is highly noise corrupted. In such cases, the estimation of the modal parameters from the input-output measurements is done based on EMA techniques. This approach however is not advisable because the operational forces due to the turbulences will appear as disturbing “noise”. Traditional EMA techniques will remove this “noise” eliminating real information. On the other hand, it has been shown that it is possible to identify modal parameters from this so-called noise contributions with an output-only approach. However, this procedure do not use the measured inputs (they are output-only data) resulting again in loss of information. In this sense, none of the EMA and OMA approaches exploit the available data in an optimal way. Clearly, to make an optimal use of the data, a new identification strategy is required. This strategy should considers the contribution to the outputs from both the measured and unmeasured forces.
In different applications the number of available outputs in a given system can be high (easily can reach dozens or hundreds). In these cases, the covariance matrix is not available or in general is difficult to obtain preventing the implementation of the maximum likelihood estimator (MLE) and restraining its use to suboptimal executions. This is inadequate since these suboptimal executions are not efficient. In this sense the developed estimators should consider the absence of the covariance matrix but still improve the estimation.
The research is focused in the modal analysis of mechanical structures where the experimentation measurements can reach easily dozens or hundreds of outputs with few inputs excitations. Nevertheless, it is important to note that this characteristic exists in different areas. Some examples are patient monitoring in medical care where the patient requires numerous sensors to asses numerous physiological parameters, in meteorology where different stations generate different data sets, in impedance spectroscopy where the sensors can be related with a particular property of a structure/tissue.